Yesterday I wrote a post that started with a quote that Charlie Munger has often used: “Invert, Always Invert.” The idea is to think differently than the crowd. Ben Graham said that our results are based on our methods, not whether the crowd agrees with us or not. However, the structure of the market is such that thinking in a contrarian way often leads us to areas that offer greater investment results. I believe that contrarianism is a necessary, but not sufficient, in successful investing.
This means thinking differently from the crowd when looking for specific investment ideas (I’m currently analyzing the for-profit education sector: talk about hated! …more on that later). It also means thinking differently in terms of overall portfolio management.
Yesterday I mentioned how one might benefit from inverting two common investment tactics: diversification and turnover. I was mostly playing devil’s advocate, because I use an adequate (but not excessive) amount of diversification, and I often hold stocks for years (just not “forever”). My style is very much rooted in classic Graham and Dodd, along with Walter Schloss’ approach to investing. My style is all about hitting base hits, one after another, and using many different transactions to compound themselves over time. This is, in my opinion, the lowest risk way to achieve excellent results.
But I often invert my thinking in order to understand how great investors achieved 50%+ returns. I will never sacrifice my risk standards, but I’m always trying to improve. In a piece on Buffett a few days ago, I mentioned how I often look at stocks and think to myself: “Will this individual investment make me money?”. This simple thinking allows you to think of the investment on its own merits, rather than just within the context of a large portfolio.
Thinking like this helps me identify my highest conviction ideas. I think Buffett thought like this. He bought Geico because he knew he had a great chance to make a lot of money in it. Same goes for Sanborn Map and other early investments. Buffett concentrated his investments, and his turnover was also much higher in his early years than it is today. The turnover aspect is an often misunderstood part of Buffett’s investment style.
Where Do Investment Returns Come From?
So after considering and weighing diversification vs concentration, and low turnover vs high turnover, I thought it would be beneficial to point out some simple, yet often overlooked, points about the math of investing, and where returns come from. This part of the post will not deal with any investment philosophy: I’m only talking about returns in a purely mathematical sense. Literally, where do returns come from?
There are only four inputs to overall portfolio returns. They are:
- Average Position Size
- Winning Percentage (% of investments that make money)
- Average Amount (%) of Winning/Losing Investments
- Number of Investments in a Given Period (Yearly if you’re interested in calculating annual returns)
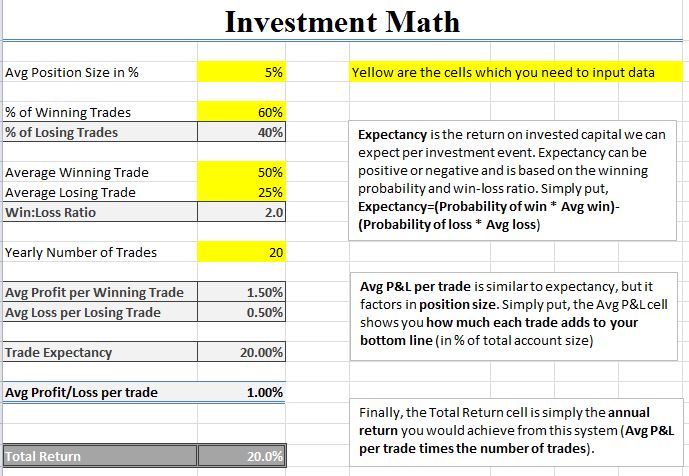
That’s it. That’s all there is to the math of investing. But most investors-value investors included-never consider this. Regardless of your style of investing, these inputs determine your output (your annual returns). For example, if you average 20 positions (5% average position size), your investments end up gaining 60% of the time (losing 40% of the time), and you average 50% on your winning trades, and 25% on your losing trades, and you make 20 trades per year, you’ll make 20% annual returns. It’s that simple.
Here is a spreadsheet I use to illustrate the above:
The yellow highlighted areas are the spots that determine your eventual results. This is just a screenshot of the sheet I have, but if you’d like a copy, just send me an email and I’ll send it to you. I created this sheet years ago, and never really use it anymore, but it’s important to understand where returns come from, because most investors don’t ever consider this. (Invert, always invert).
Once you consider the math of investing, you’ll understand that you have to have an edge in one of these areas. If you make just a few trades each year like Buffett does now, you’ll have to concentrate your investments more if you want greater than 20% returns. Or, also like Buffett, you’ll have to have a higher than 60% winning percentage. I think Mohnish Pabrai had close to 90% winning during much of his investment run of 30%+ returns from 1999-2007.
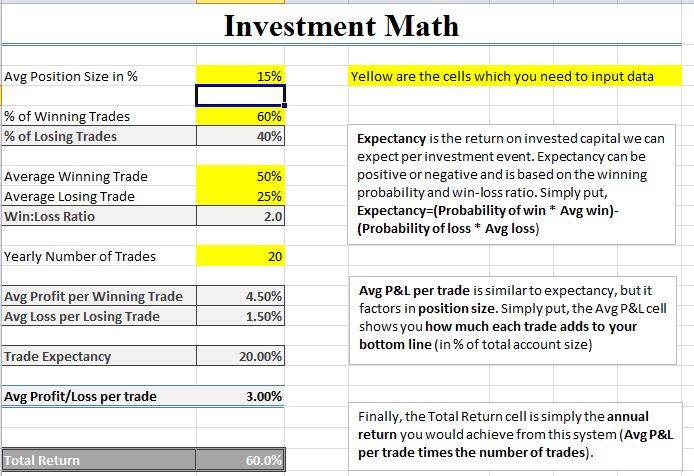
I’m not sure of Greenblatt’s turnover, but his concentration was high. He averaged 5-8 positions when he made 50% per year for a decade in his fund. Take a look at what a 15% position size does, with every other input remaining the same:
You may have guessed… it tripled the returns from the previous example. 60% per year, and around what Greenblatt achieved. So as you can see, you don’t need high turnover to achieve huge returns, but without high turnover, you need high concentration.
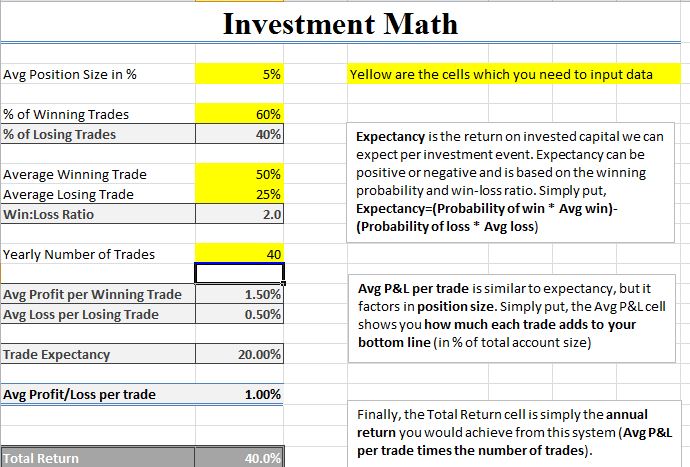
Let’s try one more example with lower concentration (5%, or a 20 stock portfolio), the same 60/40 winning percentage, but with twice as many trades (40 per year):
So in this example, higher turnover to 40 investments per year doubled the returns of the original example to 40% per year. You can also adjust the amount of your average winning/losing investments as well as the winning percentage, and that will obviously impact results.
To Sum it Up
The main point of this post is to simply consider that these four areas determine your eventual returns. I personally try to somewhat mirror the first example, attempting to achieve 20% returns by staying adequately diversified, and allowing myself to be wrong 40% of the time. My results will depend on how many investments I find that fit my criteria.
Although I prefer to hold stocks for a long time, and prefer to not trade often, I’m not afraid to turn the portfolio over more if there are more opportunities. Because I understand that my returns will increase with higher turnover, as long as everything else stays the same. Turnover gets a bad rap, mostly because average investors don’t have an edge, and they trade without rhyme or reason, and without a well-devised plan.
I also allow myself to be wrong nearly half the time, because if your strategy depends on being right 90% of the time, then you better be very convicted in your decisions. My investment style allows more room for error, and diversification both in position size, and number of investments.
Hopefully this post gives you a tidbit to think about regarding the math of investing, and how returns are created. Invert, Always Invert.
Please note: the spreadsheet is purely an example, representing hypothetical situations. None of it is a recommendation for or against those scenarios.